
Imagine a world where moving objects from one place to another isn’t just about distance but about the very fabric of space itself. This is the realm of Heisenberg group transport, a complex mathematical framework that challenges traditional Euclidean ideas. The Heisenberg group, a structure defined by intricate algebraic relationships, offers a new way to model and solve transportation problems. This approach isn’t just theoretical. It has practical applications in fields ranging from physics to urban planning. By minimizing the cost function within this unique geometry, scientists can discover optimal paths and solutions that are more efficient and adaptable than ever before.
Understanding Horizontal Divergence and Minimization
Central to Heisenberg group transport is the concept of horizontal divergence. Unlike in Euclidean space, where divergence measures the rate at which vectors spread out, horizontal divergence in Heisenberg space takes into account the group’s unique structure. The goal is to minimize this divergence while transporting objects from one point to another. This involves solving complex equations and utilizing probability measures over bounded domains. By doing so, researchers can find the most efficient ways to move objects within the Heisenberg framework, opening up new possibilities for efficient transport in both theoretical and practical applications.
The Power of Dual Formulation
One of the most fascinating aspects of Heisenberg group transport is its dual formulation. This involves transforming the original minimization problem into a dual maximization problem. By working with the dual problem, researchers can gain deeper insights and find solutions that might be difficult to identify otherwise. This dual approach also connects the Heisenberg transport problem to other well-known problems in mathematics, such as the Monge-Kantorovich problem. By exploring these connections, scientists can develop new methods and tools for solving a wide range of transport and optimization issues, further expanding the potential applications of Heisenberg group transport.
Applications and Implications in the Real World
The principles of Heisenberg group transport aren’t just confined to theoretical mathematics. They have significant real-world implications, particularly in areas that require efficient movement and allocation of resources. For example, urban planners can use these models to design more efficient traffic systems, reducing congestion and improving travel times. In physics, these concepts help in understanding particle movements and interactions at a fundamental level. By applying Heisenberg transport principles, researchers can develop more accurate models for a variety of complex systems, leading to advancements in technology and infrastructure.
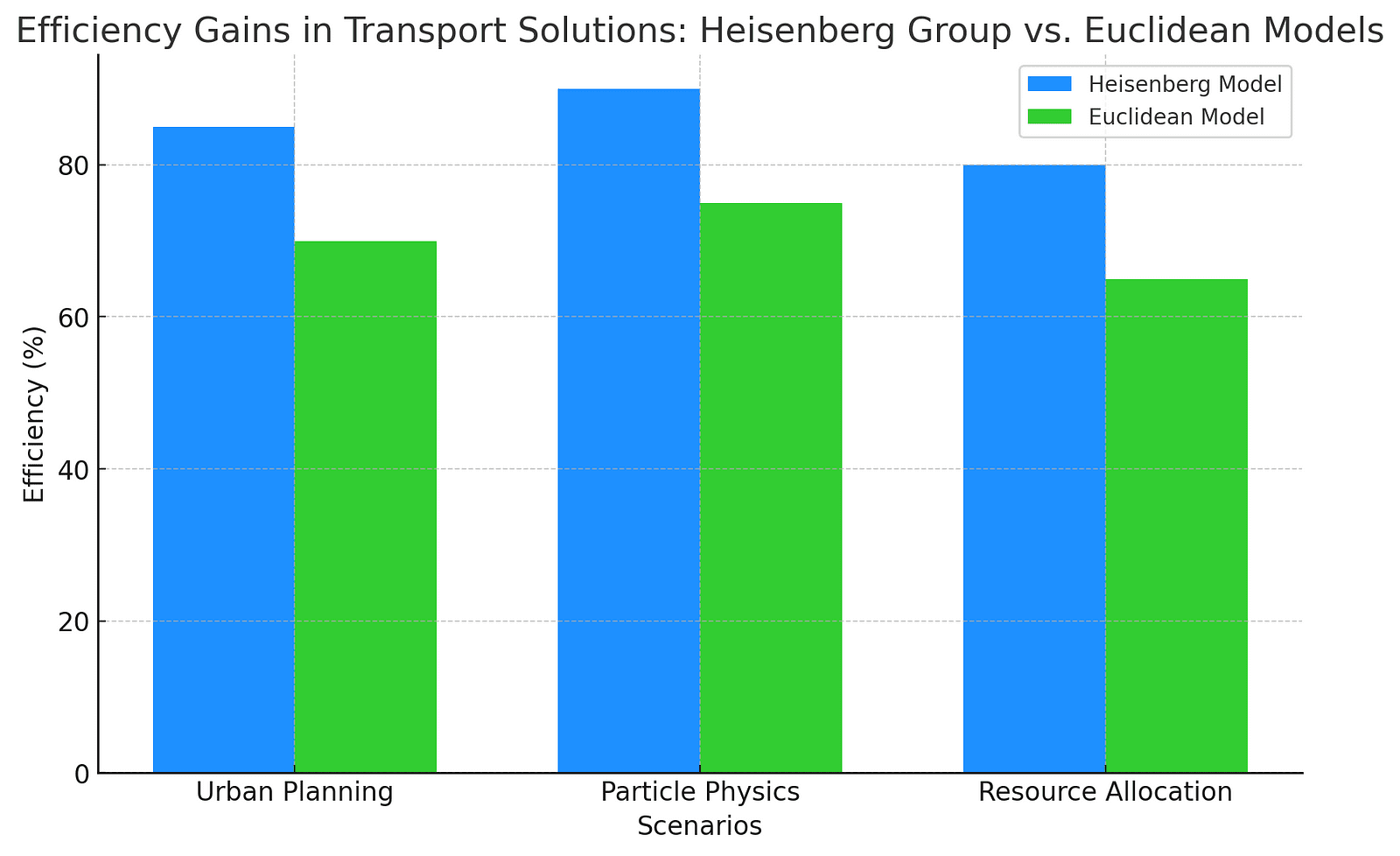
The graph below illustrates the efficiency gains in transport solutions using the Heisenberg group model compared to traditional Euclidean models
The Future of Transportation Models
As our understanding of the Heisenberg group deepens, the potential for innovative transportation models grows. Future advancements may include even more sophisticated algorithms and computational techniques to solve increasingly complex transport problems. By continuing to explore and develop these models, scientists and engineers can create more efficient and adaptable systems. This not only benefits practical applications but also enriches our theoretical understanding of space, movement, and optimization. The Heisenberg group’s unique properties offer a promising avenue for future research and development, promising a new era of efficiency and innovation in transportation.
Heisenberg Group’s Unique Geometry
The Heisenberg group is not like any regular space. Its geometry is defined by algebraic relationships that create a unique structure. This allows for more complex and efficient solutions to transport problems, making it a powerful tool in both theoretical and practical applications.
Horizontal Divergence Explained
Horizontal divergence in the Heisenberg group measures how vectors spread out within this unique space. Unlike traditional divergence, it considers the group’s specific properties, leading to more accurate and efficient transport solutions.
Dual Formulation Benefits
By transforming transport problems into their dual formulation, researchers can uncover new insights and solutions. This approach connects Heisenberg transport to other mathematical problems, expanding its potential applications and providing deeper understanding.
Real-World Applications
Heisenberg group transport principles can be applied to urban planning, physics, and resource allocation. By optimizing transport within this unique framework, we can develop more efficient systems for traffic management, particle physics, and more.
Future Potential
As research continues, Heisenberg group transport models will become even more sophisticated. This promises advancements in computational techniques and algorithms, leading to more efficient and adaptable systems in both practical and theoretical contexts.
The Horizon of Heisenberg Transportation
The future of transportation is bright with the Heisenberg group. By harnessing the power of this unique mathematical framework, we can create systems that are more efficient, adaptable, and insightful. Imagine a world where traffic flows seamlessly, resources are allocated optimally, and scientific models are more accurate than ever. The principles of Heisenberg transport are not just about moving objects but about transforming our understanding of space and efficiency. As we continue to explore and innovate, the possibilities are endless. This is the dawn of a new era in transportation, driven by the insights and applications of the Heisenberg group.
About Disruptive Concepts
https://www.disruptive-concepts.com/
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. 🚀 Subscribe for new insight videos every Saturday!
Discover the Must-Have Kitchen Gadgets of 2024! From ZeroWater Filters to Glass Containers, Upgrade Your Home with Essential Tools for Safety and Sustainability. Click Here to Transform Your Kitchen Today!







