
Dirac semimetals are special materials that have unique behaviors, especially when they reach quantum criticality. Quantum criticality is a point where a material undergoes a big change in its state, and it often involves strange behaviors that scientists want to understand. In Dirac semimetals, a special symmetry called Yukawa-Lorentz symmetry can emerge, even when the system isn’t balanced in a normal way. A new article explores what happens in these materials and how a hidden order can appear under extreme conditions.
The Tilted Non-Hermitian Dirac Landscape
Dirac semimetals are interesting because they have a linear energy relationship, which gives them something called Lorentz symmetry — kind of like how energy behaves in relativity. But what happens if we add non-Hermitian effects, which make the system interact with the environment in a way that causes energy loss? In tilted non-Hermitian Dirac semimetals, this symmetry can surprisingly survive or reappear when the system reaches a quantum critical point (QCP). The tilt in the Dirac Hamiltonian, which normally breaks the symmetry, seems to lose its impact when approaching a QCP.
This is like a chaotic group of musicians suddenly playing in perfect harmony during a big moment in a concert. The interactions in the system align, and a new symmetry emerges. This hidden order is what we call Yukawa-Lorentz symmetry, and it creates a shared velocity between different parts of the system, like fermions and bosons.
The Role of Quantum Fluctuations
Non-Hermitian Dirac semimetals are known for the strange changes they go through during quantum phase transitions. One of the key things that happens is that the tilt in the system becomes less important as we reach the QCP. This means that, even though the tilt starts by breaking the symmetry, it fades away at the critical point. Quantum fluctuations, which are like small random changes that happen at the quantum level, make all the velocities in the system line up. This is how Yukawa-Lorentz symmetry appears.
The renormalization group (RG) diagrams show that the differences in the velocities and the tilt disappear when we get close to quantum criticality. The system either becomes decoupled from the environment or keeps interacting with it while all velocities align. This result depends on whether the mass order parameter commutes or anticommutes with the Dirac mass matrix.
To make this idea clearer, the graph below shows how velocities come together in a tilted, non-Hermitian Dirac semimetal.
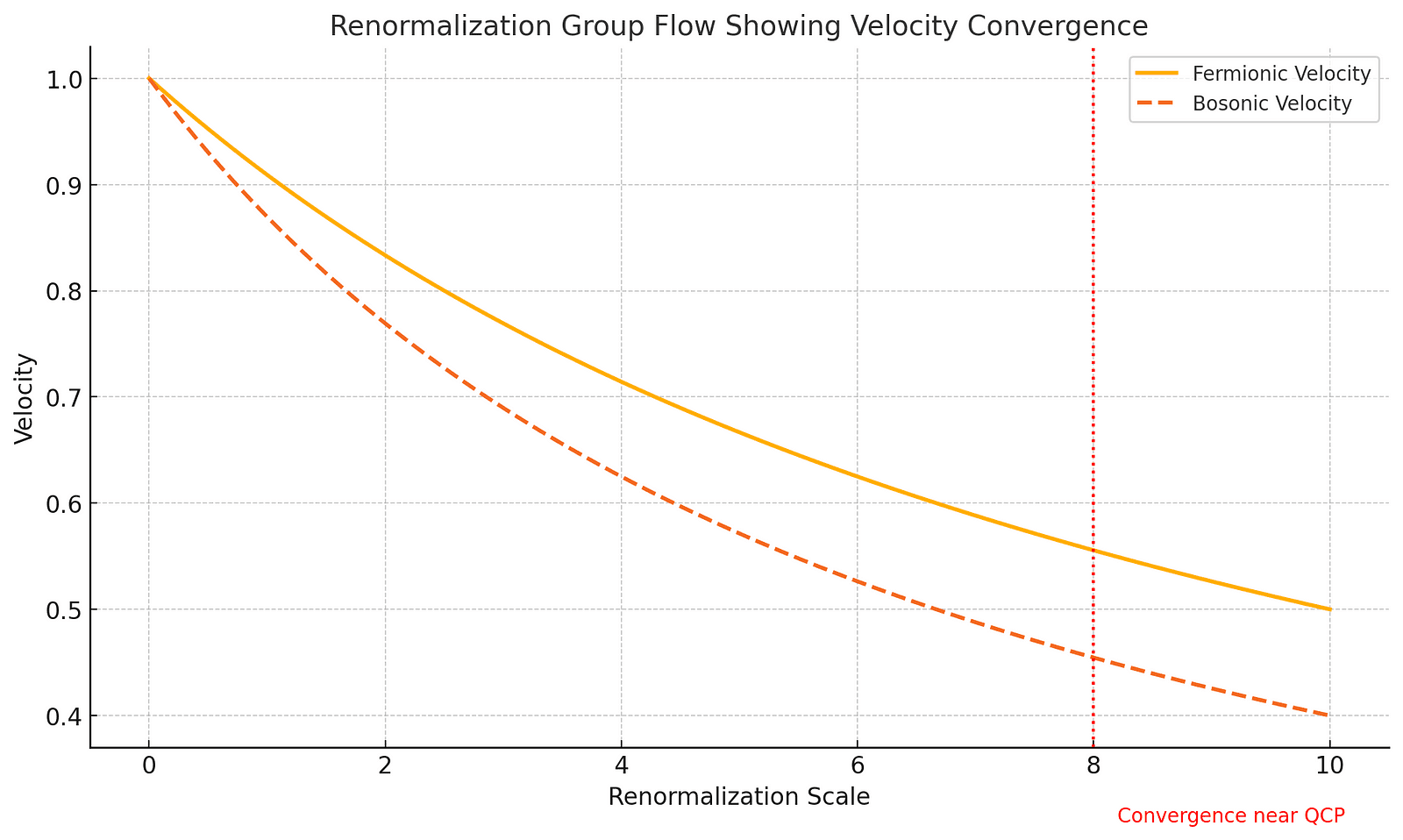
This graph shows how the speeds of different parts of the system come together as they get closer to a critical point, showing how they start to behave in sync. It helps explain how symmetry can emerge even when things initially seem unbalanced.
Emergence and Irrelevance of Non-Hermiticity
One surprising result from studying these systems is how non-Hermitian behavior changes at quantum critical points. Depending on how the mass order parameter interacts, the system either keeps its non-Hermitian properties or becomes completely decoupled, restoring normal Lorentz symmetry. If the mass order parameter anticommutes, the system completely escapes the non-Hermitian influences, like a system finding its balance again after being disturbed. This is an elegant example of symmetry coming back.
In the case of commuting mass order parameters, the non-Hermitian effects stay, but the velocities still line up. This outcome makes Yukawa-Lorentz symmetry a common feature in these systems. The system can either lose its non-Hermitian properties or keep them while maintaining aligned velocities, like a transformation that can go either way, providing insight into how symmetry and quantum fields behave.
Symmetry Appears Despite Non-Hermiticity
Yukawa-Lorentz symmetry showing up in non-Hermitian Dirac semimetals is surprising because non-Hermiticity usually breaks symmetry. At quantum criticality, though, the system realigns and the symmetry comes back, showing how stable the system can be even under tough conditions.
Tilt Becomes Unimportant at Quantum Criticality
The tilt in the non-Hermitian Dirac Hamiltonian starts by breaking Lorentz symmetry, but at the QCP, it becomes unimportant. This means the effect fades away, and the velocities of fermions and bosons end up being the same — kind of like two streams joining into one.
Two Possible Outcomes for Non-Hermiticity
Whether non-Hermiticity stays or goes depends on how the mass order parameter interacts with the system. If it anticommutes, non-Hermiticity disappears and normal symmetry comes back. If it commutes, non-Hermiticity stays but with all velocities aligned.
Yukawa-Lorentz Symmetry is Universal
This symmetry isn’t just a one-off. It appears to be a universal feature of these kinds of quantum-critical systems, which means it might also be found in other types of quantum materials. It suggests that some deep rules govern how these materials behave.
Testing the Theory in Experiments
The predictions about Yukawa-Lorentz symmetry can be tested in experiments, especially with quantum Monte Carlo simulations and non-Hermitian lattice models. If scientists can see the velocities coming together in these experiments, it would prove the symmetry and show how stable it is.
The Yukawa-Lorentz Ubiquity: A Broader Context
The idea of Yukawa-Lorentz symmetry in non-Hermitian Dirac materials isn’t just a theory. It can be tested with experiments like quantum Monte Carlo simulations and studying non-Hermitian lattice models. The fact that the tilt becomes unimportant suggests that these symmetry properties might not depend heavily on starting conditions. This is a powerful idea because it hints that these kinds of symmetries could also appear in other non-Hermitian systems.
This universality makes us wonder if similar symmetries exist in other areas of condensed matter physics. For example, could non-Hermitian versions of Weyl or Majorana fermions also show symmetry restoration during quantum phase transitions? It might be that there’s a general rule that applies to many different exotic phases.
Finding Order in Chaos
Order at Quantum Criticality
As we explore non-Hermitian Dirac semimetals, we see that even in the most chaotic quantum systems, there is order. At quantum criticality, new kinds of symmetry appear, breaking the usual ideas of how systems should behave. The way all velocities come together — whether or not the system keeps its non-Hermitian properties — shows how quantum fluctuations can lead to unexpected harmony.
The discovery of Yukawa-Lorentz symmetry invites us to look deeper and understand how quantum fields align under critical conditions. Just like watching a group of birds form a perfect V-shape in flight, these semimetals at critical points show us that quantum systems have an instinct for order, even when it seems like everything should be in disarray.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. 🚀 Subscribe for new insight videos every Saturday!
See us on https://twitter.com/DisruptConcept
Read us on https://medium.com/@disruptiveconcepts
Enjoy us at https://disruptive-concepts.com
Whitepapers for you at: https://disruptiveconcepts.gumroad.com/l/emjml







