
What happens when the seemingly simple world of graph theory collides with the enigmatic properties of surfaces? Negami’s planar cover conjecture, proposed in 1988, posed an elegant challenge: Can every connected graph with a planar cover embed on the projective plane? Over decades, mathematicians have extended this question to surfaces of higher genus, uncovering tantalizing connections between topology and combinatorics. This question is not only a theoretical pursuit but also has practical implications. Understanding these embeddings can advance fields like computational topology, network design, and data visualization, where the interplay of structure and space is critical. Over decades, mathematicians have extended this question to surfaces of higher genus, uncovering tantalizing connections between topology and combinatorics. As researchers expand these conjectures to encompass orientable and non-orientable surfaces, the implications grow profound. This article dives into the mathematical odyssey of embedding graphs on surfaces, exploring groundbreaking discoveries that reveal the hidden structure of graphs in higher dimensions.
The Origins: Negami’s Planar Cover Conjecture
The story begins with the conjecture that a connected graph has a finite planar cover if and only if it can embed on the projective plane. This premise drew from a deep topological insight: The sphere serves as a double cover for the projective plane, creating an intuitive bridge between planarity and embeddability. Negami’s conjecture garnered significant attention, with progress focusing on a single unresolved case: the graph. Despite partial resolutions over decades, no finite planar cover for this graph has been found.
However, the richness of the conjecture lies in its adaptability. By broadening its scope to surfaces of varying genus, researchers introduced a new dimension to this puzzle. The fundamental question evolved: If a graph has a cover embeddable on a surface Σ, can the graph itself embed in Σ? Extending this principle to orientable and non-orientable surfaces revealed intricate relationships between graph structure and surface topology.
Breaking Boundaries: The Generalized Conjecture
In 1999, Hliněný proposed a generalization: For every compact surface Σ, a connected graph has a finite Σ-cover if and only if it is embeddable in Σ. This conjecture, now encompassing orientable and non-orientable surfaces, reframed the challenge as a unifying principle in topological graph theory. For instance, orientable surfaces of higher genus posed unique hurdles, as some graphs with planar covers demonstrated arbitrarily high genus.
A pivotal breakthrough came with the development of bounding functions for Euler genus — a measure of a surface’s complexity. Researchers proved that connected graphs with finite covers embeddable in Σ exhibit bounded Euler genus, providing critical constraints to test the conjecture. This theoretical leap illuminated new pathways for decidability, surpassing earlier progress on the original planar conjecture.
Insights from Structural Graph Theory
The generalization of Negami’s conjecture owes much to structural graph theory, particularly the role of minors and their relationship to embeddability. A graph is a minor of if can be derived through edge deletions, vertex deletions, or edge contractions. Kuratowski’s theorem — characterizing planar graphs by forbidden minors — laid the foundation for exploring minor-closed classes of graphs.
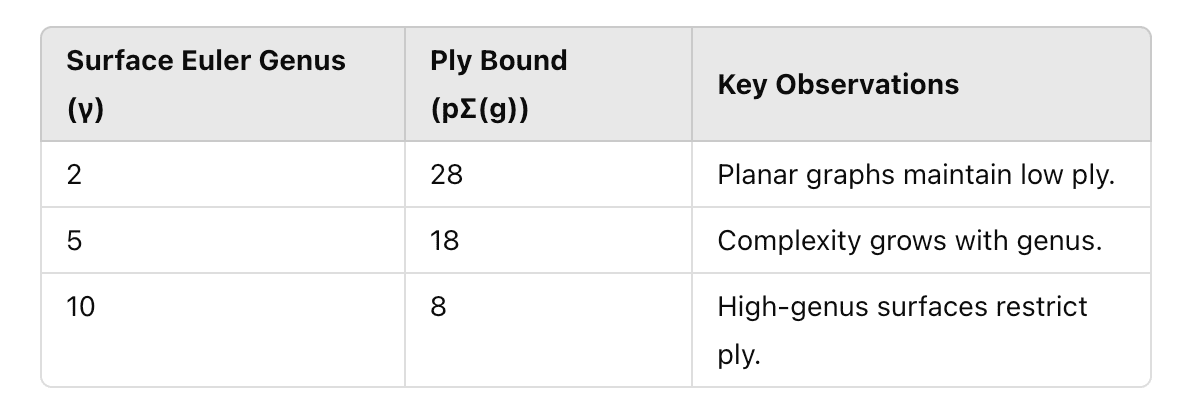
In the higher-genus context, the study of so-called “sum-Kuratowski graphs” emerged as critical. These graphs, derived from combinations of classical Kuratowski graphs ( and ), embody structural properties that determine embeddability on surfaces of varying complexity. Leveraging Robertson and Seymour’s graph minor theory, researchers demonstrated that graphs with sufficiently high Euler genus inevitably contain specific sum-Kuratowski graphs as minors. This insight proved instrumental in bounding the ply — a measure of cover size — for graphs embeddable on higher-genus surfaces.
To visualize the relationship between Euler genus and ply, consider the following table summarizing key insights:
How Surfaces Guide Embeddability
Surfaces dictate embeddability through genus and orientability, with higher-genus surfaces providing more embedding options but tighter restrictions.
The Role of Forbidden Minors
Graphs excluded as minors, like and , delineate boundaries for embeddable graphs, particularly for compact surfaces.
Why Ply Matters
Ply defines the complexity of a graph’s cover. Lower ply simplifies embedding verification, crucial for both planar and higher-genus surfaces.
Decidability Across Dimensions
Unlike Negami’s planar conjecture, generalized conjectures for high-genus surfaces offer algorithms for decidability, though they remain computationally intensive.
Applications Beyond Graph Theory
These findings extend to computational topology, enabling advancements in network design, data visualization, and algorithmic geometry.
A Future on the Horizon
The journey to proving Negami’s conjectures across dimensions illustrates the evolving interplay between combinatorics and topology. As researchers push the boundaries of decidability and embeddability, they open doors to applications in physics, data science, and beyond. The unifying principles behind finite covers and surface embeddings promise a deeper understanding of graph structures in multidimensional spaces. What began as a question of planarity now illuminates a broader landscape, inviting exploration into the infinite potential of mathematics and its real-world implications.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. 🚀 Subscribe for new insight videos every Saturday!
See us on https://twitter.com/DisruptConcept
Read us on https://medium.com/@disruptiveconcepts
Enjoy us at https://disruptive-concepts.com
Whitepapers for you at: https://disruptiveconcepts.gumroad.com/l/emjml







