
Brownian motion, named after the botanist Robert Brown, is a fascinating phenomenon where particles suspended in a fluid move randomly due to collisions with molecules in the fluid. Imagine observing pollen grains in water under a microscope, jittering erratically without any apparent reason. This seemingly chaotic motion is actually a predictable and well-studied process in physics and mathematics. Brownian motion is not just a random path but a window into the underlying structure of randomness itself. Understanding this motion helps scientists and engineers design better materials, forecast financial markets, and even understand biological processes at a molecular level.
The Geometry of Random Paths
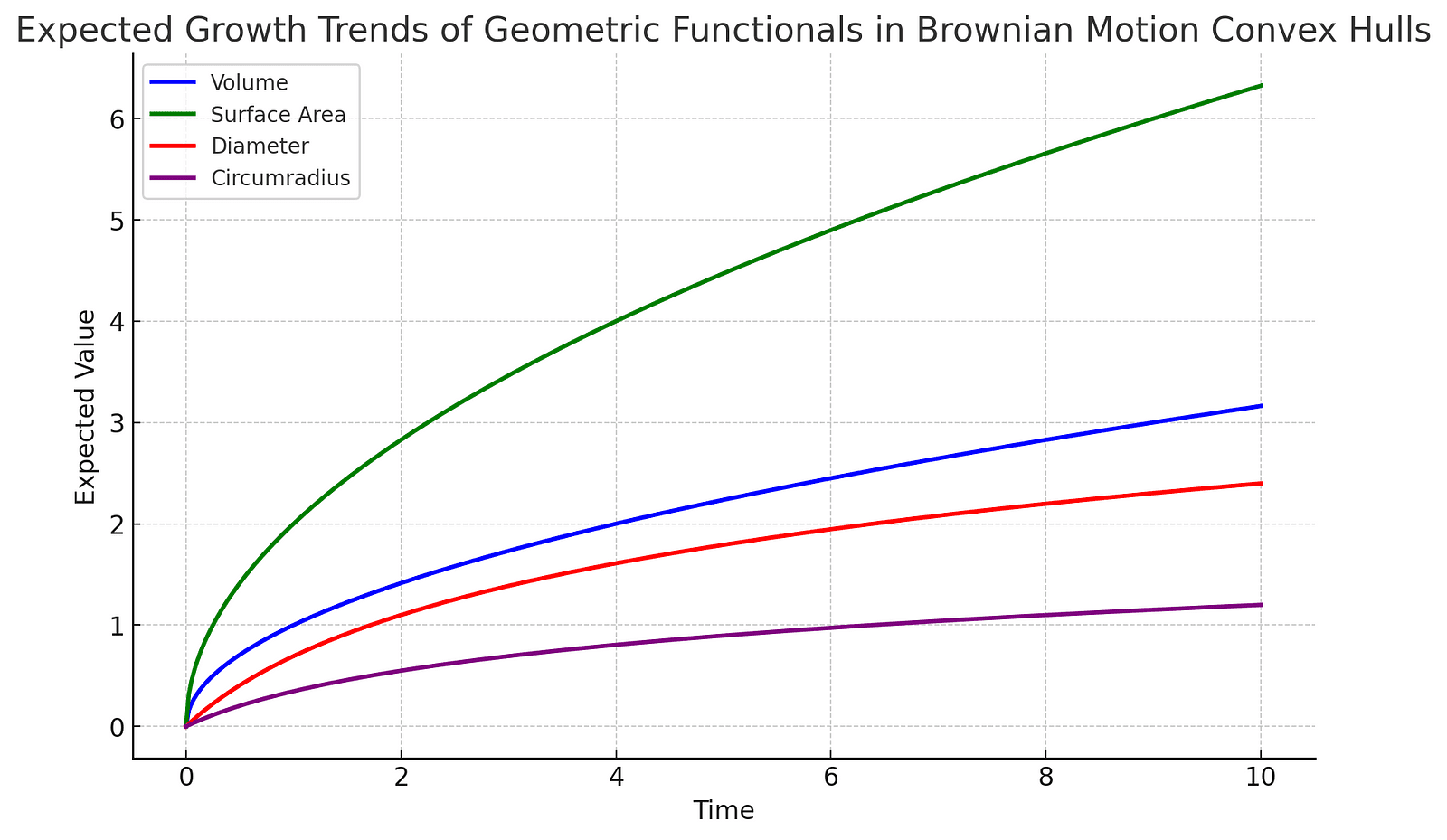
When we talk about the convex hull of Brownian motion, we’re referring to the smallest convex shape that can encompass the entire path of a particle. In higher dimensions, this concept becomes even more intriguing. Imagine a particle moving in a 3D space, and now extend that to four, five, or even more dimensions. The geometric functionals like volume, surface area, diameter, and circumradius of these convex hulls provide insights into the nature of high-dimensional spaces. These metrics help in understanding how quickly these shapes grow, their boundaries, and their overall structure, which has applications in fields ranging from data science to quantum physics.
To further illustrate the concept of the growth of geometric functionals in Brownian motion, we can visualize the expected values of the volume, surface area, diameter, and circumradius over time.
A Measure of Speed
Inverse processes tell us how long we must wait for a geometric functional, like volume or surface area, to exceed a given value. This is akin to asking, “How long does it take for the convex hull to become large enough to cover a certain area?” These processes are crucial in fields that rely on time-based measurements and predictions. For instance, in finance, it can relate to the time required for an asset’s price to reach a certain level. In physics, it helps in understanding diffusion processes. The study of these processes in high dimensions extends our knowledge from the familiar three-dimensional world to more abstract, yet fundamentally important, higher-dimensional spaces.
Why This Matters
The research on Brownian motion and its convex hulls in high dimensions is not just a theoretical pursuit. It has practical implications in numerous fields. For instance, in computer science, algorithms that deal with large datasets often operate in high-dimensional spaces. Understanding the behavior of Brownian paths can improve these algorithms, making data processing more efficient. In physics and chemistry, this knowledge helps in the study of molecular behavior and the development of new materials. Even in everyday technology, from smartphones to AI systems, the principles derived from this research play a role in enhancing performance and capabilities.
The Universal Scaling Law
Brownian motion follows a universal scaling law where the path’s length increases proportionally to the square root of time. This fundamental principle is used to model various natural phenomena, from the diffusion of particles in liquids to stock market fluctuations.
Fractal Nature of Paths
The paths traced by Brownian particles are fractal-like, meaning they are self-similar at different scales. This property is why Brownian motion is a cornerstone in the study of fractals and chaos theory, impacting fields like meteorology and geology.
Einstein’s Insight
Albert Einstein’s 1905 paper on Brownian motion provided empirical evidence for the existence of atoms and molecules. His work laid the groundwork for modern statistical mechanics and thermodynamics, transforming our understanding of matter.
Applications in Medicine
Understanding Brownian motion is critical in medicine, particularly in drug delivery systems. Nanoparticles designed to navigate the bloodstream rely on principles of Brownian motion to reach targeted areas within the body, improving treatment efficacy.
Financial Markets
Brownian motion models are extensively used in finance to predict stock prices and market trends. The random walk theory, based on Brownian principles, suggests that stock price movements are unpredictable in the short term, influencing investment strategies worldwide.
A Future Full of Possibilities
The exploration of Brownian motion and its geometric properties in higher dimensions opens doors to new technologies and scientific breakthroughs. By understanding the intricacies of random paths, we can develop more robust algorithms, design better materials, and even improve medical treatments. The research doesn’t just stay within the confines of theoretical physics or pure mathematics; it permeates through various aspects of our lives, subtly enhancing the technology we use and the scientific principles we rely on. This continuous journey into the depths of randomness promises not just new knowledge but new ways to harness that knowledge for the betterment of society.
About Disruptive Concepts
https://www.disruptive-concepts.com/
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. 🚀 Subscribe for new insight videos every Saturday!
Discover the Must-Have Kitchen Gadgets of 2024! From ZeroWater Filters to Glass Containers, Upgrade Your Home with Essential Tools for Safety and Sustainability. Click Here to Transform Your Kitchen Today!







