
Think of a digital photo. When you zoom in, it becomes a bunch of squares, right? That’s pixelation. Now, imagine mathematical functions and relations as pictures. Normally, they’re smooth, like a curve. What this research does is similar to zooming in on these curves until they become a series of steps or blocks. This is a big deal in math because it’s like translating a high-definition movie into a form that even an old TV can display without losing the plot. It makes complex, continuous models (those without breaks) into simpler, discrete ones (with distinct jumps), which is super handy for understanding and using these models in real-life situations.
To help you visualize the concept of ‘pixelating’ a mathematical function, here’s a graph below showing a smooth, continuous curve and its pixelated version.
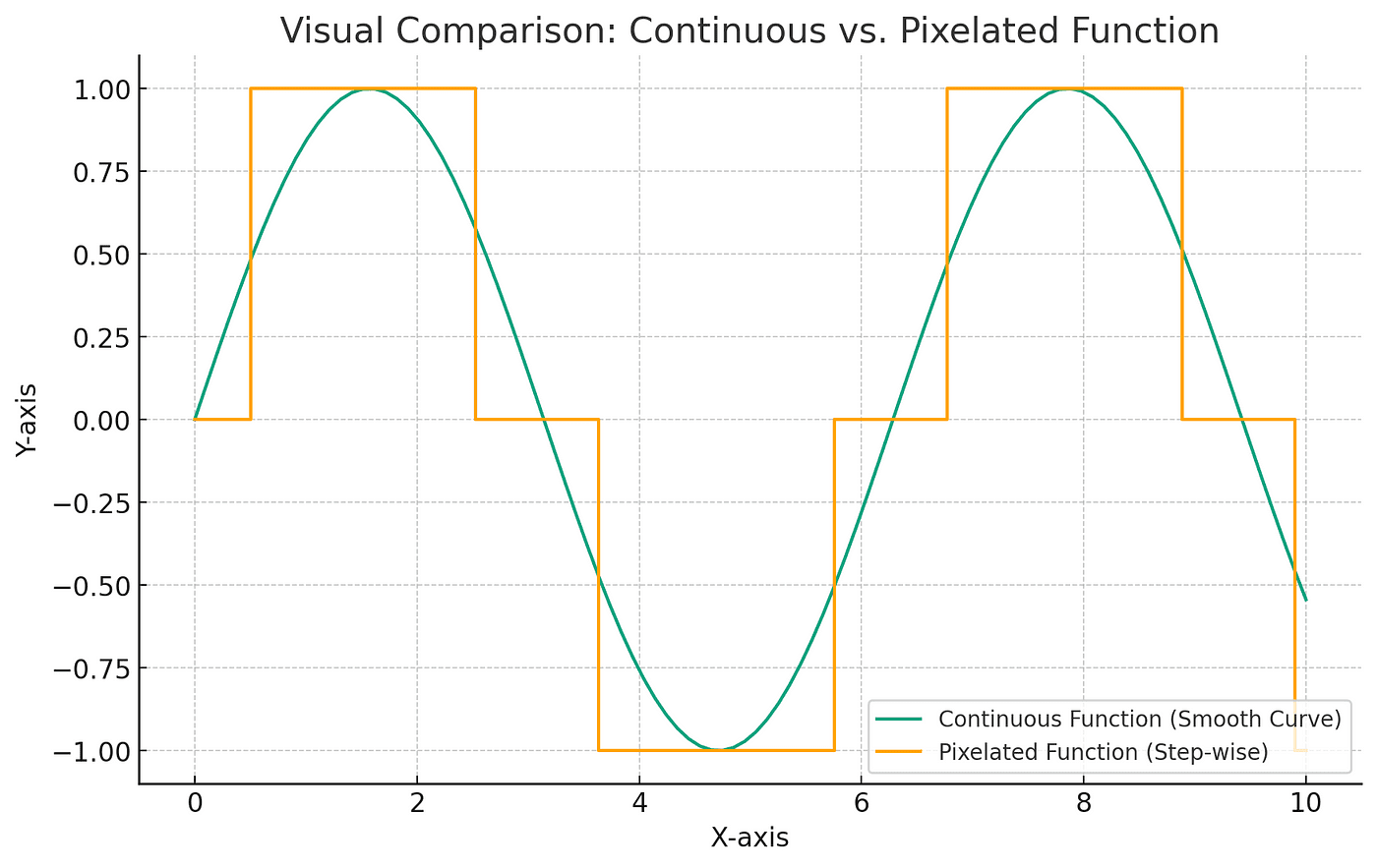
Simplifying the Complex Without Losing Essence
It’s like taking a really intricate story and retelling it in simpler words without missing the main points. The paper explores methods to do this with mathematical models, ensuring that while they’re made easier to understand, their core information remains intact. Imagine explaining a complex movie plot to a friend in just a few sentences, yet they still get the whole picture. That’s what this research is about — retaining the critical elements of complex mathematical functions and relations while presenting them in a more straightforward, digestible form.
Bridging Two Mathematical Worlds
In the math universe, there are two realms: the continuous (like a smooth line) and the discrete (like a dot-to-dot drawing). Typically, these two don’t mix much. But what if you could seamlessly connect them? That’s what this research is about. It finds a way to represent continuous models, which are usually complex and infinite, in a discrete, simpler form. It’s like translating a continuous melody into individual notes that still carry the tune’s essence.
A Mathematician on a Mission
The Author isn’t just a mathematician; he’s like a translator between different mathematical languages. He dives deep into the world of combinatorics, graph theory, and the algorithmic aspects of property testing. His work focuses on making complex mathematical concepts more accessible, which can be a game-changer not only for fellow mathematicians but for students and professionals in various fields.
Why This Research Matters
The driving force seems to be making the complex simple, and the infinite comprehensible. Imagine having a super complex recipe and breaking it down into just a few easy steps without losing the dish’s essence. This kind of simplification can revolutionize how we deal with data in computer science, tackle long-standing math problems, and even change the way we teach and learn complex mathematical concepts.
Capturing Infinity in a Finite Way
The research provides a method to represent infinite mathematical models in a finite, comprehensible way. This is like capturing the boundless expanse of the ocean in a single, clear snapshot. It’s a concept that sounds almost magical — taking something as vast and unending as infinity and making it understandable and manageable. In practical terms, this can revolutionize how we approach problems in various fields, from physics, where understanding the infinite is often crucial, to computer science, where managing large, seemingly endless streams of data is a daily challenge. This breakthrough in simplifying the infinite not only makes it more approachable for academic study but also potentially impacts real-world applications, such as in algorithms and data analysis, where grappling with vast amounts of data is common.
Applications Beyond Mathematics
The implications of this research extend far beyond the realm of mathematics. In the digital world, where data compression and image processing are fundamental, the ability to simplify complex data without losing essential information is invaluable. This could lead to more efficient storage of data, faster processing times, and even more detailed and accurate digital imaging. In a world that increasingly relies on digital technology, from smartphones to medical imaging devices, these advancements could have a profound impact. Imagine being able to store more photos on your phone without losing quality, or doctors being able to see more detailed images during medical diagnoses. This research blurs the line between the abstract world of mathematics and practical, everyday technology.
A New Approach to Old Problems
The Author’s methodology might offer novel solutions to age-old mathematical problems. By breaking down complex continuous models into simpler, discrete representations, mathematicians can gain new perspectives on these problems. It’s akin to taking a jigsaw puzzle and rearranging the pieces in a way that makes the picture clearer. This new approach could potentially unlock answers to mathematical mysteries that have remained unsolved for years, providing a fresh set of tools for mathematicians worldwide. Moreover, this approach could inspire a new generation of mathematicians, showing them that even the most daunting problems can be approached in creative, unconventional ways.
A Ripple Effect Across Disciplines
The potential impact of this research is not confined to mathematics alone; it ripples across multiple disciplines. In physics, for instance, understanding complex systems is crucial, and this research could provide new ways to model these systems more simply. In economics, where models often involve predicting human behavior, a simplified yet accurate model could lead to better forecasts and decision-making. The ability to break down complex systems into understandable components can be a game-changer in any field that relies on data and models. This interdisciplinary impact underscores the universal nature of mathematical concepts and their power to influence a wide range of human endeavors.
Redefining Mathematical Education
This research could dramatically change how complex mathematical concepts are taught and understood. By simplifying intricate ideas into more digestible forms, it opens the door for a broader range of students to engage with advanced mathematical concepts. Imagine a classroom where topics that once seemed daunting are now approached with confidence and curiosity. This could lead to a deeper, more intuitive understanding of mathematics, encouraging more students to pursue STEM fields. Furthermore, this approach could help bridge the gap between theoretical mathematics and practical applications, showing students the real-world relevance of what they’re learning.
A Bright Future Ahead
What this paper offers is not just a remarkable mathematical achievement; it’s a promise of a future where complexities are made simple and accessible. It inspires hope for innovations that can streamline how we process information, revolutionize education, and uncover solutions to problems we’ve yet to solve. In essence, the work is about making the seemingly incomprehensible, comprehensible, not just to the math whizzes, but to anyone with curiosity and a willingness to explore the universe of numbers.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your crystal ball into the future of technology. 🚀 Subscribe for new insight videos every Saturday!







